10人に1人当たるデジタルくじ。2回引いて、2回とも当たる確率は?

今度発売する製品の販促案なんですが、製品にQRコードをつけて、くじ引きをするのはどうでしょうか。当たるとキャラクターオリジナルのデジタルスタンプがもらえるとか。大体、1人につき2個程度、購入していただけるのを想定しています。

いいかもね。どのくらいの確率で当たることを想定しているの?

(確率っていわれても、ふわっとしか分からない! なんて答えればいいのかな…? まあいいか)
10人に1人です!

なるほど、10%の確率か。当たりやすいね。

(話がつながった!)
そうです、10%です! そして、商品を2個買っていただいたとき、2回とも当たる確率は20%ですよね? すごいたくさんの人が当たりますよ! 満足度爆上げです。

ん? 2回とも当たる確率は0.01だから1%だね。

え?(なんでーーー?どうしてーーー?)
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
どう計算したの? そこに登場した、大人向け数学教室大人塾を運営し、数学苦手な社会人に対して指導をしているモリさん。

この記事を読むべき人:確率の意味を理解していない方
この記事を読む必要がない人:確率の基本をすぐに算出できる方
この記事でわかること:確率の基本、積の法則の利用、和の法則の利用、余事象
確率とはなんだ!

モリさん、確率ってそもそもなんでしたっけ?

確率とは、あることがらが起こる可能性の度合いのことです。

あることガラガラポン?

(ガラガラポンふるっ! アユムさん、もしかして昭和っ子?)
落ち着いて。確率の王様といえば、降水確率ですね。

たしかに。降水確率ってほぼ毎日聞いたり目にしたりしますよね。一喜一憂することも多いです。

降水確率は、過去の同じような気象状況の情報をもとに算出しているんですよ。降水確率30%とは、30%の予報が100回発表されたとき、そのうち30回は雨が降る可能性があるという意味です。

降水確率って、そういうことなんですね。考えたことなかったです。ところで先輩が「10人に1人が当たるのは10%」っていってましたが、確率って割合なんですか?

確率は、起こる可能性の度合いです。一方で割合は、事実がベースの計算です。なので、実際に当たった人を調べて「10人中1人が当たりました」というのが割合、「10人中1人が当たるでしょう」という想定の計算が確率です。意味的には近いですね。

10%が0.1であることはわかるんです。が、10%っていったり、0.1といったり、言い方が定まっていないんですよね。一体確率ってどういう風に表すんですか?

学校では分数で習いますね。分数だと、考えやすく、意味がよくわかります。また、分子÷分母で小数になるので、先輩のいう「0.1」は「 1 10」の言い換えですね。確率の数字が小さい場合、100倍して%とするほうが伝わりやすくなります。今回なら 1 10×100=10% ですね。●%や●割は、こういうときに使います。

で、確率はどう求めるんですか?

ことがらが起こる場合の数 すべての場合の数 で表します。だから、分数にすると意味をイメージしやすいんです。

はい、順列や組み合わせでは、場合の数を用いて、何通りあるかを数えました。確率も、場合の数と同じ考え方です。

ことがらが起こる場合の数、というのは、何か特定の場合ということですか?

はい、例えば「A、B、C、D、Eさんからなる5人のグループから、くじ引きで役員1人を決めるとき、Aさんが選ばれる確率は?」という問題があったとします。Aさんが選ばれる場合の数は、何通りですか?

Aさん1人なので、1通りですね。

では、誰かが役員となる場合の数は、全部で何通りですか?

全部で5人なので、5通りですね。

ということは?

ことがらが起こる場合の数 すべての場合の数 なので 1 5であってますか?

その通りです!
もう1つ、私がよく行く居酒屋さんでは、お魚、お野菜、お肉のいずれかのお通しが出ます。お通しは全部で10種類、そのうちお魚のお通しが3種類あるとします。お通しをくじ引きで選ぶとき、お魚のお通しに当たる確率は?

お通しがくじ引きで決まるっておもしろいですね。モリさんがお魚のお通しに当たる確率は、 ことがらが起こる場合の数 すべての場合の数で 3 10ですね!

その通りです。 ことがらが起こる場合の数 すべての場合の数が確率の基本になることを覚えておきましょう。
120%おかしい? 確率は「100%」つまり「1」を超えない

そういえば、確率と割合は似ているといいましたが、確実に違う点があります。確率は「1」つまり「100%」を超えることはありません。

え? そうなんですか? 「120%当たる!」みたいなのってありません?

たとえば、当たる確率が120%だとすると、分数に直して 12 10になりますよね。
このとき、すべての場合に当たる数が10通り、ことがらが起こる場合に当たる数はいくつですか?

12ですね。

はい。では「10回引いたら当たりがいくつか?」というケースで、「10回引いたら当たりが12回出ます」となるのは、おかしいですよね。

確かに! その2回はどこから? 120%おかしいですね。

そうです。なので確率が絡む話題で「120%」などと出てくるときは、100% 誇張表現や詐欺です。気をつけてくださいね。

100%! 100%って全部ってことですか?

その通り、いいですね。「10回引いたら10回当たり」の計算はどうなると思いますか?

ことがらが起こる場合の数 すべての場合の数 = 10 10 = 1 つまり100%ですね!

ばっちりです!まとめましょう。ことがらが起こる確率は1を超えません。かつ、最大でも1です。しっかり、肝に銘じておいてください。それでは、唱えましょう。

\確率は1を超えない/
2回連続で当たる確率は?(積の法則の利用)

ところで、先輩に、10%のくじを2回引いて2回とも当たる確率は20%だといったら、違うと言われました。どうしてでしょうか。

なるほど。いい質問ですね。まず、外れる確率はどれだけですか? いろいろな都合上、小数で回答していきましょう。

外れる場合の数が9通りで、すべての場合の数は10通りなので、 9 10(0.9)ですね。


そうか、1回目と2回目って連続してますね。

連続といえば? ゴホンゴホン

(わざとらしいセキだなぁ)
あ、積の法則! 前回教えてもらいましたね。

すばらしいです。連続している場合は積の法則を利用して掛け算ですね。つまり、2回引いて2回とも当たる確率は 0.1×0.1=0.01 です。つまり、1%!

1%! 100人に1人が2回連続で当たる! 少なそうで、多くもないですね! 2回連続で当たりが出たら、嬉しくなって2個以上買いそうですね!

そうですね。いい確率計算の活用方法ですね。確率がわかると、どういう風に販促に活用するかイメージしやすくなりますね。

はい!
「少なくとも」の確率は?(余事象)

ところで、外れる確率の0.9って、当たる確率の0.1を1から引いたのと意味は同じですか?それって、 前回教えてもらった余事象?

すばらしい着眼点ですね。その通り、これはアジアゾウではなく余事象(ヨジショウ)です。すべての確率は1なので、そこから引いた確率と、外れの場合の数を出して計算した確率は同じですね。

はっ、モリさんがゾウさんに!

確率の余事象をもう少し考えましょう。2回引いて、2回とも当たらない場合の確率は?

当たらない確率が0.9なので、2回とも当たらないのは、0.9×0.9=0.81ですね。

では2回引いて、少なくとも1回当たる確率は?

「少なくとも1回当たる」は「2回とも当たらない」の余事象なので、1-0.81=0.19。いかがでしょうか!?

ゾーウ(正解)!
パターンごとの確率は?(和の法則の利用)

へへっ! これは、ワァ~~の法則で検算できるんでしたっけ?

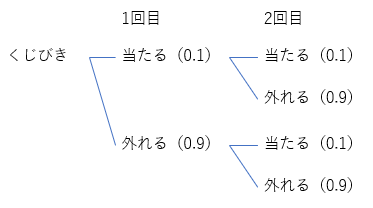
ワァ~~ではなく、和の法則です。足し算ですね。先ほどの樹形図に戻ります。
それぞれの起こる確率を求めましょう。


少なくとも1回以上当たる確率というのは、上から3つを足すんですね。0.01+0.09+0.09=0.19 ワァ~~!

はい、和の法則で、少なくとも1回以上当たる確率を求められますね。これで、余事象で求めたときと同じ答えになりました。

ワァ~~!

ゾォ~~ゥ!(精いっぱいの対抗)

ビジネス書を読んでいて確率と出てくると、勝手に震えていたんですが、そんなに怯えることもなかったですね!

はい、確率= ことがらが起こる場合の数 すべての場合の数 ということをわかっていれば、確率の基本は、恐るるに足りずってとこですね。
ポイント
- 確率は、
ことがらが起こる場合の数 すべての場合の数 で求める。 - 連続している(同時に起こる)ときは、積の法則を利用する
- パターンに分けて考えるときは、和の法則を利用する
- 特定の事象が起こらないことを考えるときは、余事象
今日の問題をおさらい
Q1 10人に1人当たるデジタルくじ。2回引いて、2回とも当たる確率は?
0.1×0.1 = 0.01
答え:0.01(または 1 100)
Q2.10人に1人当たるデジタルくじ。2回引いて、2回とも当たらない人の確率は?
当たらない確率 1-0.1 = 0.9
0.9×0.9 = 0.81
答え:0.81
Q3.10人に1人当たるデジタルくじ。少なくとも1回当たる確率は?
- 余事象で求める
1 - 1回も当たらない確率 = 1-0.81 = 0.19
- 和の法則で求める
2回当たる確率 0.01
1回だけ当たる確率
1回目当たり × 2回目外れ 0.1×0.9 = 0.09
1回目外れ × 2回目当たり 0.9×0.1 = 0.09
0.01+0.09+0.09 = 0.19
答え:0.19
※このコンテンツはWebサイト「Web担当者Forum - 企業Webサイトとマーケティングの実践情報サイト - SEO・アクセス解析・SNS・UX・CMSなど」で公開されている記事のフィードに含まれているものです。
オリジナル記事:10%の確率で当たるデジタルくじ。2回引いて、2回とも当たる確率は?|確率をゼロから学ぼう | 算数が苦手なマーケター向け「算数基礎講座」
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.