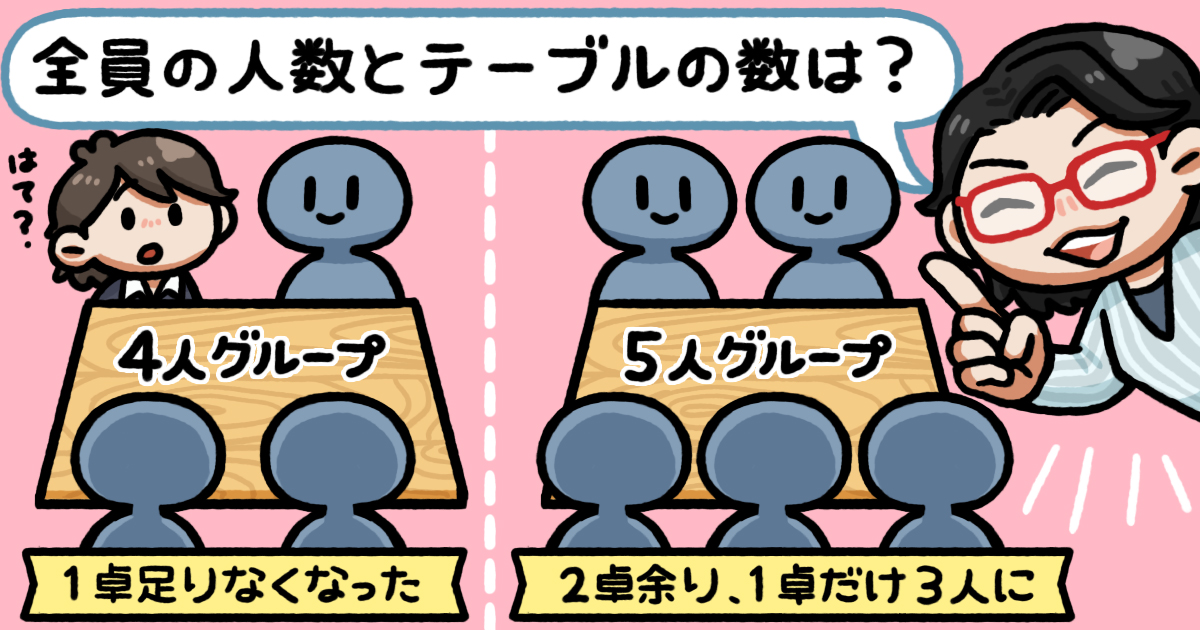
参加者数は何人? テーブルは何卓?

久しぶりにグループワークの研修を実施をするんだ。

いいですね! ワーク形式は楽しいですよね~。

ところが、4人ずつグループにすると、テーブルがちょうど1卓足りなくて、5人ずつグループにするとテーブルは2卓余るし、最後のグループは3人になってしまう。悩ましいね。

参加者は何人なんですか?

参加者は68名、テーブル数は16個だね。ちなみに、先ほどの条件で、参加者数とテーブル卓数が求められるよ!

え? そんなことができるんですか? どうやって?

ヨシ、考えてみよう! ではまた!

えええええ!?
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているアジアゾウをこよなく愛するモリさん。
この記事を読むべき人:「余る」「足りない」などの 条件から全体を計算することが苦手
この記事を読む必要がない人:過不足算を解ける方
この記事でわかること:条件から全体を求めること、絵をかくこと
情報を整理してテーブルの数と人数を求める

モリさん、テーブルにつけない人の数から、全員の人数って割り出せるんですか?

ずいぶん唐突ですね。まぁ、いつもそうですが。今日はどうしましたか。

今度、先輩がグループワーク形式の研修をするんですって。で、4人ずつグループになるとテーブルが1卓足りなくて、5人ずつグループになると、テーブルが2卓余って、最後のグループが3人になってしまうそうなんです。で、全部で何人で、テーブルがいくつあるかといわれたのですが、求め方が皆目見当つきません。

なるほど。となると、何かを 𝒳 とおきましょうか。

何を𝒳とおくかって、悩むんですよね。う~ん、全部の人数を𝒳とおきますか?

悩みますよね。今回は、卓数を𝒳にしたほうがよいですね。というのも、慣習的に、𝒴=a𝒳+b という式にしたいなと考えます。1卓に何人ずつつく、という計算式を作ると想定したときに、全部の人数はテーブルの卓数𝒳 とテーブルについた人数のかけ算で出せるからです。

なるほど。では、全部の人数を𝒴とおきます。

本当は、きちんと式を立てて計算できれば、なにを𝒳,𝒴とおいても、いずれ、文字は消えますので、何をどの文字で置いたかをメモしておけばどうにかなります。悩むくらいなら、文字をエイヤとおいて式を作ったほうが効率が良いです。

ふーん、そんな軽い感じでいいんですね。

さて、では、4人ずつテーブルにつかせてください。人数𝒴はどうあらわせますか?

4人×テーブル卓数𝒳=4𝒳 の人数がテーブルにつけますね。

そして、人が余ってますね。

ちょうど1卓足りないということは、何人余ってるんでしょう?

わかりづらいときは、絵にしてみましょうか。

え! 自分、絵をかくの下手なんですが…。

芸術品をかいてほしいわけではないので、ご安心を。四角と丸だけで情報を整理しましょう。
4人ずつテーブルについていって…、1卓足りないということは、最後の4人にはテーブルがない!


なるほど、テーブルにつけない人数は4人です。わかりやすいです。

つまり、人数𝒴=4𝒳+4 になりますね。ちなみに、アユムさん、ここでは余った4人を足した結果として式にしましたが、足りないテーブルで考えると、どうなりますか?
「足りない」をあらわす

え、1卓足りないので、𝒴=4(𝒳-1) になるのではないですか?

ちがいますね。それでは、足りないということについて考えましょう。

足るを知るってやつですか。

それ足りているほうですね。絵にしてみましょうか。
はじめに考えたように、テーブルの数𝒳でそのまま人数を考えると、テーブル卓数分の人数 4𝒳 に加えて、足りてない1卓分の4人を足す式 𝒴=4𝒳+4 になります。


そうですね。そう考えました。

ですが、あと1つあれば全員がテーブルにつけると考えて、𝒳に+1 とすると…。


𝒳+1卓のテーブルに4人ずつなので…、なるほど。𝒴=4(𝒳+1)でも、人数をあらわせますね!

その通りです。足りない、なので -1 としてしまうと、ミスのもとです。今回の場合、テーブルから考えるときは、足りないを補うために +1となります。足りないときに、足すのか引くのか悩むときは単位を意識しながら式を作りましょう。
「余る」をあらわす

1つ式ができたので、今度は5人グループのほうを式であらわしたいです!

では、アユムさん、式を作ってみましょう。

5人ずつグループになると、テーブルが2卓余って、最後のグループが3人になってしまう。テーブル数が𝒳で、人数が𝒴なので…混乱するなあ。

まず、一つひとつ情報を整理していきましょう。状況を把握するために絵をかきますね。
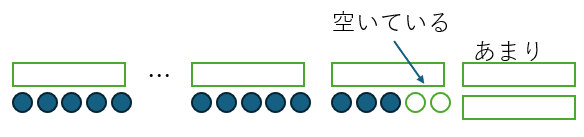
5人グループのテーブルはいくつですか?

全部のテーブルが𝒳卓で、2卓余るので𝒳-2卓ですか?

最後のテーブルは3人グループという話ですね。となると、「5人つくテーブル」は?

そうか、𝒳ー3卓になるのですね。

ということは、5人ついたテーブルにいる合計人数は?

5人×(𝒳-3)卓で、5人グループの人数がわかりますね。

で、さらに3人いるんですよね。

ということは、𝒴=5(𝒳-3)+3 とあらわせます。

その通り! では、4人のときのように、違う見方もしてみましょう。2卓を除いて、全員が5人のグループになっているとすれば?

5人×(𝒳-2)卓で、人がいるテーブル全部に5人座っているとあらわせますね。

いいですね。

でも、実際は2人足りないんですよね。
となると、𝒴=5人×(𝒳-2)-2 ですか?

その通り! こちらも、同じ式にたどりつきますが、起点が違うだけで、2通りの式から見ていくことができますね。

4人グループの場合、𝒴=4𝒳+4
5人グループの場合、𝒴=5𝒳-10-2=5𝒳-12
2つの式ができました。

では、それを計算して、卓数𝒳を求めましょう。

4𝒳+4=5𝒳-12 より、𝒳=16

では、人数を求めましょうか。

4×16+4=68人 5人グループのほうで計算しても 5×16-12=68人! 先輩の答えとも一致しました!

ばっちりです。このように、1つの状況を複数の視点からとらえることで、2通りの式で表せます。違う見方から立てられた式を見て「なるほど~、こういう考え方もできるのか」となるのは、算数の楽しみでもあります。

算数が楽しいっていう人は、考え方が色々あるのが好きと、よく言いますよね。

そうなんです。

楽しさはわかったのですが、余っているとか、足りないとかの表現で間違えそうです。

そのようなときは、何が余っている、何が足りないということをしっかりと認識し、しっかり言葉にすることが大切です。絵をかくのもよいでしょう。そして、それらを式にしましょう。算数を学ぶことが論理的思考を学ぶことと同じであるといわれるのは、筋道を立てて考える練習ができるからですね。

なるほど~
応用問題に挑戦! 全体の人数と長椅子の数は?

それでは、もう1問挑戦してみましょうか。
あるイベントにて、6人ずつ長椅子に座ったところ、全体の3/4しか座れませんでした。
そこで、3脚増やし、7人ずつ座ったところ、最後の長椅子には1人分のスペースが余りました。
さて、長椅子の数と全体の人数を求めましょう。

えーと、長椅子の数を𝒳、人数を𝒴とおきます。

はい。

全ての長椅子に6人ずつ座って全体の3/4なので、6𝒳=3/4𝒴 、𝒴=8𝒳 でいいですか?

絶好調ですね。よくそのポイントをクリアしました!

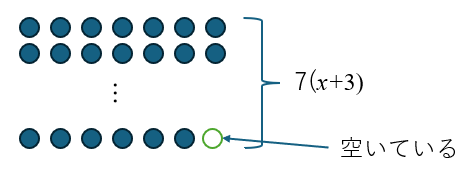
次に、3脚増やしたので、𝒳+3脚になったということですね。それに7人ずつ座ったので、7×(𝒳+3)=𝒴 ですか?

そして、1人分のスペースが余っていますね。

余っているということは…7×(𝒳+3)のほうが全体の人数より1多いということですよね。

いいですね!

ということは、1を引かなくてはいけないので、7×(𝒳+3)-1=𝒴 まとめると、7𝒳+20=𝒴

すばらしい!

では、求めまーす。𝒴=8𝒳 と 7𝒳+20=𝒴 よって、8𝒳=7𝒳+20、𝒳=20

長椅子の数が求められましたね。

つまり人数は、8×20=160人です。

すばらしい! よくできました!

この余るとか足りないって、やはり苦手です…。

いま自分が何を数えているのか、その値が何を示すのかをしっかり考えましょう。絵をかいてもよいでしょう。

ひるまず、しっかり考えるようにします!

ところで、これ、全員、空気椅子とかだったら面白いですね。

そんなの想像するだけで、絵面が怖すぎます。
ポイント
- 足りない、余る問題は、何が余っているのかなどをしっかり考える
- 混乱しそうだったら絵をかく
- 値が何かを意識する。特に単位を意識するとよい
今日の問題をおさらい
Q1. 研修にて、4人ずつグループにすると、テーブルがちょうど1卓足りなくて、5人ずつグループにするとテーブルは2卓余るし、最後のグループは3人になる。テーブルの卓数と人数を求めよ。
テーブルの卓数を𝒳、人数を𝒴とおく。
𝒴=4𝒳+4
𝒴=5(𝒳-3)+3
これを解いて
𝒳=16(卓) 𝒴=68(人)
答え:テーブル16卓、参加者数68人
Q2. あるイベントにて、6人ずつ長椅子に座ったところ全体の3/4しか座れませんでした。
そこで、3脚増やし、7人ずつ座ったところ、1席余りました。
さて、長椅子の数と人数を求めましょう。
長椅子の数を𝒳、人数を𝒴とおく。
6𝒳=3/4𝒴 を解いて、𝒴=8𝒳
7×(𝒳+3)-1=𝒴 を解いて、7𝒳+20=𝒴
8𝒳=7𝒳+20、𝒳=20 𝒴=160
答え:長椅子20脚、参加人数160人
※このコンテンツはWebサイト「Web担当者Forum - 企業Webサイトとマーケティングの実践情報サイト - SEO・アクセス解析・SNS・UX・CMSなど」で公開されている記事のフィードに含まれているものです。
オリジナル記事:【計算できる?】4人ずつは1卓足りず、5人ずつは2卓余り、1卓だけ3人に…参加人数とテーブル数は? | 算数が苦手なマーケター向け「算数基礎講座」
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.


